CAPITOLUL 5

 

5.1. Descrierea metodei

 

                 Folosirea metodei Monte - Carlo presupune asocierea unui model stochastic, procesului (fenomenului) ce urmează a fi analizat. Metodologia folosită este următoa­rea:

       a) se stabileşte numărul variabilelor aleatoare ce se iau în considerare, X₁, ... , X_n

       b) pentru fiecare variabilă 13 se face un număr de observaţii. Se fac apoi studii statistice pentru a le estima cu abatere cât mai mică în probabilitate în raport cu cele considerate reale. În final pentru fiecare variabilă se va specifica distribuţia statistică;

       c) pe baza unor procedee de generare a numerelor aleatoare sau pseudoaleatoare se generează şiruri de numere aleatoare sau pseudoaleatoare cu distribuţii corespunză­toare distribuţiilor estimate anterior;

       d) ţinând seama de modelul elaborat şi de obiectivul ales, se aplică metode matema­tice adecvate pentru a pune în evidenţă, cu ajutorul acestor şiruri, diferite variante posibile şi/sau soluţii rentabile. Se face apoi studiul statistic al valorilor funcţiei scop sau al valorilor ce trebuie estimate;

       e) dacă abaterea medie pătratică este mai mare decât cea impusă, se măreşte numărul termenilor şirului în scopul obţinerii unui grad de precizie dorit.

       Metoda Monte - Carlo este strâns legată de problemele teoriei probabilităţi­lor, statis­ticii matematice şi analizei numerice. Ea se distinge prin simplitatea şi generali­tatea ei. Neajunsul metodei îl constituie convergenţa lentă, este vorba de convergenţa în probabilitate, specifică problemelor ce admit o descriere probabilis­tică. Acest neajuns se înlătură uneori prin modificarea procedurii de calcul permiţând obţinerea unui ordin de înaltă convergenţă.

       Majoritatea schemelor metodei Monte Carlo se bazează pe legea numerelor mari (Bernoulli) pentru variabilele aleatoare independente.

       Fie ξ₁, ..., ξ_n variabile aleatoare independente şi identic repartizate. Presupunem că media M(ξ_k) = a < ¥ şi dispersia D(ξ_k) = σ² < ¥ (k=1,...,n). Notăm cu . În acest caz, pentru (") ε > 0 este verificată inegalitatea lui Cebîşev

                                                                                              (5.1)

ceea ce este echivalent cu inegalitatea

                                                                                         (5.2)

       În ipotezele date avem:

oricare ar fi 17 şi α > 0 arbitrare, pentru n suficient de mare, media aritmetică se va abate de la a cu o mărime cel mult 1 - α.

       Legea numerelor mari este însă valabilă şi în ipoteze mult mai slabe. Astfel, în forma dată de Hincin

                 când n ® ¥ în condiţiile existenţei unei valori medii finite pentru variabila aleatoare ξ. În acest fel, are loc convergenţa în probabilitate a mediei aritmetice 20 către valoarea medie M(ξ) în cadrul unor ipoteze mai puţin restrictive. Dacă dispersia D(ξ_k) este infinită atunci inegalităţile (5.1) şi (5.2) sunt lipsite de sens, fiind însă valabilă inegalitatea

                  

unde ξ_k sunt variabile aleatoare independente, nu neapărat identic repartizate, dar având aceeaşi valoare medie, a.

În simularea Monte Carlo prezintă interes nu numai convergenţa variabilei către valoarea medie M(ξ) ci şi repartiţia ei. Dacă σ² < +¥ şi există momentul centrat de ordinul al treilea , atunci teorema limită centrală afirma că repartiţia lui este  asimptotic normală, cu dispersia şi media a, adică se verifica inegalitatea:

                    

unde C₀ este o constantă absolută, despre care se ştie că 0,9051 > C₀ ³ .

       Tehnica Monte-Carlo presupune aşa cum am arătat un experiment statistic efectuat pe un model artificial al fenomenului real.

       Să considerăm că variabila aleatoare X a modelului real are dispersia σ² finită şi media μ de asemenea finită.

       Să presupunem că modelul artificial este supus experimentului statistic în N cicluri de simulare. În cadrul fiecărui ciclu de simulare având nevoie de n valori ale variabilei aleatoare X.

       Deci X = {X₁, X₂, ..., X_N}

unde X_j = {x_j1, x_j2, ..., x_jn} (") j=1, ..., N.

       Fie .

       Construim variabila aleatoare  cu valorile posibile ₁, ..., _N numită media de selecţie. Atunci reprezintă estimaţia absolut corectă pentru media teoretică μ.

       Mărimea 30 se numeşte eroare. Cu ajutorul ei se poate defini eroarea relativă .

       Conform legii numerelor mari, variabila aleatoare  M() tinde spre μ iar din inegalitatea lui Cebîsev vom avea că

În aplicaţii  (de obicei k = 2 sau k = 3) ceea ce înseamnă că .

       Mărimea poartă numele de nivel de semnificaţie.

Cu aceste notaţii avem că .

       Conform teoremei limită centrală vom avea ca variabilă aleatoare M() are o repartiţie normală , rezultă că: .

       Dacă se fixează un α suficient de mic şi se pune ,

atunci se obţine:

       , adică, cu probabilitatea de cel puţin 1 - α, media aritmetică a realizărilor independente ale lui _j diferă de μ cu cel mult . Pentru α şi σ fixaţi, eroarea descreşte cu N^-1/2.

       Dacă dorim să determinăm numărul N al ciclurilor de simulare necesare pentru ca probabilitatea: să fie de 0,95 atunci din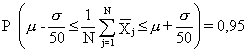

avem ca:

      

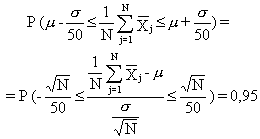
       Variabila 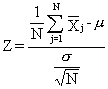urmează o lege normală de medie 0 şi dispersie 1. Din tabela funcţiei Laplace vom determina valoarea lui astfel încât 47. Găsim astfel că . Aceasta înseamnă că N » 10 000.