3.6.3. Teoria lui Bayes şi ponderile probelor

Presupunem că trebuie să alegem între două sau mai multe ipoteze H₁, H₂, ..., H_n (n ³ 2), şi avem proba (dovada) E în ajutorul informaţiei de bază (iniţiale) B. Probabilităţile P(H_i/B) (i = 1, 2, ..., n) sunt cunoscute ca probabilităţi anterioare sau iniţiale (anterioare luării în considerare a probei E, dar în mod necesar anterioare apariţiei cronologice a lui E), şi P(H_i/BÇE) sunt cunoscute ca probabilităţi posterioare sau finale.

Apoi, eliminând posibilitatea probabilităţii f, rezultă imediat din axiome că

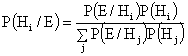
şi este cunoscută ca teorema lui Bayes, deşi el nu a folosit notaţiile moderne.

Este interesant cum o teoremă atât de simplă poate avea consecinţe cu o bătaie atât de lungă. Lucrarea lu Bayes a fost publicată postum, fiind găsită printre hârtiile sale de către Price care a avut contribuţii la publicare. Faptul că Bayes nu a publicat teorema în timpul vieţii are mai multe explicaţii posibile, una fiind aceea că poate nu era satisfăcut de partea lucrării legată de valorile probabilităţilor anterioare.

, sau unde l nu depinde de i, este numită posibilitatea lui H_i având E, astfel, teorema lui Bayes poate fi exprimată în forma: "probabilitatea posterioară a lui H_i este proporţională cu probabilitatea anterioară a posibilităţii" (Jeffreys, 1939).

Când probabilităţile subiective sunt utilizate în statistică, împreună cu teorema lui Bayes, abordarea se numeşte bayesiană sau neo-bayesiană. Metodele ne-bayesiene se mai numesc şi metode de frecvenţă sau metode ale teoriei înregistrărilor baye.

Rata şanselor posterioare faţă de cele anterioare pentru H este cunoscută ca "factorul Bayes", faţă de H asigurat de E.

Logaritmul său este uneori numit ponderea dovezilor (probelor) în favoarea lui H oferite de E, B dat, şi se poate nota W(H:E/B). Baza logaritmilor defineşte doar unitatea în termenii căreia această pondere este măsurată.

Pentru baza 10, Turing a numit unitatea ban, o zecime deciban. Decibanul este aproape cea mai mică unitate a unei ponderi a dovezilor pe care mintea umană o poate înţelege şi este analog decibelului din acustică.

Pentru a justifica expresia "pondere a dovezii" în acest sens tehnic, să ne imaginăm că H reprezintă vina unui om acuzat şi negaţia lui H motivaţia lui, şi fie E dovezile prezentate la judecător. Fie W₁(H:E) ponderea dovezilor în favoarea vinei (vinovăţiei)oferite de dovada E singură (deşi avem şi alte informaţii la bază), unde aici "pondere a dovezii" trebuie interpretată în sensul intuitiv şi ordinar (obişnuit) de balanţă a dovezii (nu ca sumă a părţilor favorabile şi nefavorabile ale dovezii). În formaţia de bază B poate fi inclusă în notaţie scriind W₁(H:E/B) dar îl vom omite pe B pentru simplificarea expunerii. Următoarele necesităţi apar natural:

i) W₁(H:E) trebuie să depindă numai de P(E/H) şi P(E/-H);

ii) P(H:E) trebuie să depindă numai de W₁(H:E) şi de probabilitatea iniţială P(H).

Se poate demonstra că W₁(H:E) trebuie să fie o funcţie de W(H:E). Putem la fel de bine să luăm W₁ = W pentru că avem dorita proprietate de aditivitate.:

Factorii Bayes au o corespondentă proprietate multiplicativă, dar, atunci când discutăm despre "ponderi" aditivitatea este mai potrivită.

Este necesar ca magistraţii, oamenii din juriu şi doctorii care pun diferite diagnostice, să ia în considerare cel puţin judecăţi implicite sauprobabilităţi finale de forma P(H/E), probabilitatea ipotezei, atunci când dovada Eeste asigurată.