CAPITOLUL 5

 

Metoda Monte - Carlo

 

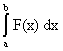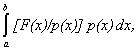       Termenul de "Metoda Monte - Carlo" se utilizează pentru a desemna două tehnici diferite. Prima tehnică constă în evaluarea integralelor definite prin utilizarea variabilelor aleatoare. Obiectivul este de a calcula  (unde x poate fi un vector), estimând expresia unde p(x) este funcţia de densitate a variabilei aleatoare definită pe [a,b]. În acest caz, problema iniţială este transformată în aceea privind estimarea mediei lui F(x)/p(x). Aceasta se poate rezolva generând valori aleatoare pentru p(x) şi apoi calculând media lui F(x)/p(x).

       Al doilea sens al "metodei Monte - Carlo" presupune înlocui­rea unui fenomen real cu un experi­ment statistic, ce va fi studiat cu ajutorul tehnicilor moderne de calcul. Variabilele aleatoare ce intervin în model, sunt gener­ate cu calcula­torul prin procedee adecvate. În vederea obţinerii unei imagini corecte a evoluţiei fenomenului sau procesului studiat trebuie ca variabilele aleatoare să fie estimate cu abatere cât mai mică în raport cu cele ce apar în realitate şi experimentul să fie repetat de un număr convenabil de mare de ori, pentru a se pune în evidenţă principa­lele trăsături ale fenomenului modelat.

       Această metodă cuprinde în realitate mai multe tehnici de simulare în cadrul cărora analiza fenomenului real se înlocu­ieşte cu analiza unui fenomen artificial, descris de un model, prin rezolvarea acestuia generând pentru variabile, valori aleatoare.

       Deci, metoda asociază problemei reale un model aleator şi prin generarea unor variabile aleatoare legate funcţional de soluţie, se realizează experienţe pe model şi se furnizează informaţii asupra soluţiei problemei deterministe. Dintre domeniile pentru care se pretează utilizarea metodei Monte - Carlo menţionăm:

- Cercetările operaţionale: studiul sistemelor de servire; gestiunea stocuri­lor; metoda PERT; jocuri operaţionale.

- calcul numeric: rezolvarea integralelor multiple; rezolvarea ecuaţiilor diferenţiale; probleme Dirichlet.

- economie: studiul gestiunii materialelor; jocuri de conducere; dezvoltarea unei ramuri, zone, economii; procesul de repartiţii şi de producţie.

- industrie: procese de muncă; repartiţia optimă a utilajelor; probleme de transport.

- alte domenii: biologie, chimie, mecanica fluidelor, fizica nucleară, fenomene naturale, etc.

       Metoda îşi demonstrează eficienţa în analiza fenomenelor şi proceselor care se produc în sistemele caracterizate printr-un număr foarte mare de variabile şi parame­trii, prin relaţii complexe între componente, prin factori perturbatori şi prin modificări a evoluţiei în timp.

       Folosirea acestei metode nu impune cu necesitate cunoaşterea relaţiilor exacte dintre mărimile ce urmează a fi estimate, ci este suficient să fie pus în evidenţă acel complex de condiţii în prezenţa cărora experimentul respectiv are loc.

       Bazele teoretice ale metodei au fost puse în anul 1949 de Metropolis şi Ulam, dar ideea acestor metode a apărut încă din 1777 când Buffon a formulat celebra problemă a calculului probabilităţii de intersecţie a unui ac aruncat la întâmplare, pe o suprafaţă plană pe care sunt trasate drepte paralele echidistante, idee care în 1860 datorită lui Barbier a permis calculul numărului π prin aruncări succesive ale unui ac de lungime l, pe o suprafaţă plană cu drepte paralele la echidistanta a. Fermi, Metropolis şi Ulam foloseau pentru aplicarea metodei, la studiul difuziei neutronilor în materialele fisio­nabile, listele de numere întâmplătoare care se publicau la Monte - Carlo. De aici a rezultat cea mai răspândită denumire a metodei. În SUA metoda a mai fost cunoscută şi sub denumirea de "metoda Las Vegas". În literatura de specialitate se întâlnesc următoarele denumiri echiva­lente: metoda încercărilor echivalente; metoda experimentărilor statistice; simularea numerică; metoda simulării indirecte; metoda numerelor aleatoare.