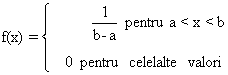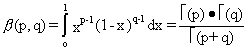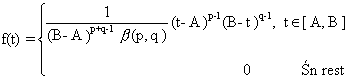CAPITOLUL 6
6.5. Determinarea duratei optime
de execuție a unui proiect
Metoda PERT (Program Evaluation and
Review Techique) încearcă să țină seama de variațiile duratelor de execuție a diverselor
activități dintr-un graf de tip ADC. În acest scop,
metoda permite calcularea timpului mediu de terminare a unui proiect,
identificarea activităților critice precum și estimarea probabilităților de
realizare a termenelor planificate.
Metoda se aplică
îndeosebi la proiecte din domeniul cercetării și dezvoltării. Ea pornește
de la următoarele ipoteze:
a) pentru
fiecare activitate a unui graf G, atașat unui proiect dat, se poate estima durata optimistă (durata minimă de
execuție a unei activități) aij; durata
cea mai probabilă (durata cu cea mai mare șansă de realizare) mij
și durata pesimistă bij
(este intervalul de timp maxim de realizare a activității (i,j));
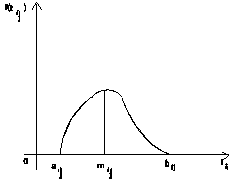
b) durata
fiecărei activități a proiectului are o distribuție beta:(fig.6.9)
Densitatea de repartiție
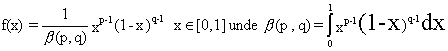
|
|
Așa
cum se vede, distribuția beta satisface condițiile care au un
suport practic solid, bazat pe următoarele observații:
- intersectează
axa abciselor în două puncte care pot corespunde duratelor aij și bij;
- este
unimodală, adică are o singură valoare maximă care poate corespunde duratei mij;
- valoarea
(bij - aij) este intervalul de variație al distribuției
și poate indica gradul de împrăștiere al duratelor posibile.
c) durata
medie de execuție tij a unei activități (i,j) este dată de:
![]() ; (6.12)
; (6.12)
d) dispersia
duratei tij de execuție a activității (i,j) se calculează cu
ajutorul relației:
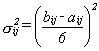 (6.13)
(6.13)
Dispersia reprezintă o măsură a
gradului de nesiguranță în estimarea duratei de execuție activității (i,j); o valoare mare a acesteia înseamnă o mare nesiguranță
în privința duratei reale de execuție;
e) durata
totală a proiectului este o variabilă aleatoare cu distribuție normală a cărei
medie tn și dispersie σn2 sunt:
![]() (6.14)
(6.14)
![]() (6.15)
(6.15)
unde Dcrit reprezintă mulțimea tuturor arcelor
rețelei G care sunt pe drumul critic;
f) probabilitatea
de realizare a duratei planificate Tplan a unui proiect se determină
calculând mai întâi factorul de probabilitate Z după relația
![]() (6.16)
(6.16)
Și
apoi se deduce din tabelul valorilor funcției
g)
graful trebuie să conțină un număr suficient de mare
de activități pentru a întruni toate condițiile aplicării teoremei limită
centrală iar duratele activităților sunt variabile aleatoare independente.
Teorema
limită centrală.
Fiind dat un șir de
variabile aleatoare independente X1, X2, ... Xn,
cu dispersiile σ12, σ22,
...σn2, dacă dispersiile sunt finite și suma lor
crește indefinit cu n, dar astfel încât fiecare raport σ22/
![]() σi2 --> 0 atunci
variabila
σi2 --> 0 atunci
variabila ![]()
urmeaz_, la limită, o lege
de repartiție normală redusă, oricare ar fi distribuția variabilelor Xi.
Aceasta
înseamnă că o sumă de variabile aleatoare independente, fiecare dintre ele
având o repartiție oarecare, urmează, dacă numărul acestor variabile este suficient de mare, o lege normală (legea
Gauss-Laplace), a cărei medie este suma mediilor variabilelor și a cărei
dispersie este suma dispersiilor variabile.
4) dacă
sunt definite termene planificate de finalizare pentru fiecare activitate (Tij),
probabilitatea ca fiecare activitate să fie executată la termenul planificat se
determină calculând factorii de probabilitate zij, după formula:
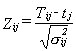 (6.17)
(6.17)
unde tj
este termenul minim de terminare al activității (i,j). Apoi, utilizând tabelul valorilor funcției
Calculul
unui program PERT. Presupunem că s-a trasat rețeaua unui proiect și că pentru durata
fiecărei activități avem trei estimări aij, mij, bij;
Procedura
de calcul
folosește etapele:
1. Se calculează durata medie a
fiecărei actibvități a rețelei utilizând relația (6.12);
2. Se calculează termenele
evenimentelor tj după procedeele ADC cunoscute, considerând duratele
activităților determinate și egale cu mediile lor;
3. Se calculează dispersia duratei
fiecărei activități utilizând relația (6.13);
4. Se determină tn
și σn2 cu ajutorul relațiilor (6.14) și (6.15);
5. Se determină probabilitatea de
realizare a duratei planificate a proiectului după relația (6.16) și a
tabelului valorilor funcției
6. Se analizează, în final,
probabilitatea calculată la punctul 5 șinând seama de următoarele criterii:
- dacă p(tn
£ Tplan) este
aproximativ mai mică decât 0,25 există un mare risc de a nu se realiza
proiectul la termenul planificat și deci e necesar să se revizuiască duratele
de execuție în sensul urgentării lor;
- dacă p(tn
£ Tplan)
» 0,5 programarea este justă;
- dacă p(tn
£ Tplan) este
aproximativ mai mare ca 0,6 programarea utilizează excesiv anumite resurse.
7. Dacă sunt date termenele
planificate de execuție a fiecărei activități a proiectului, atunci se
calculează și probabilitățile ca fiecare activitate să
fie executată la termenul planificat. În acest sens se
utilizează rela_ia (6.17) și tabelul valorilor funcției
Analiza acestor probabilită_i se face
dup_ cum urmează:
- dacă pij
(ti
£ Tij) este aproximativ mai mică decât
0,6 atunci trebuie luate măsuri de urgentare a executării activității (i,j) în
vederea realizării ei în termenul planificat;
- dacă pij
(t
£ Tij)
³ 0,6 atunci avem o justă planificare
a execuție activității (i,j).
Exemplu. Considerăm un
proiect format din 15 activități (fig.6.10).
Rezolvarea prin metoda PERT a
grafului este dată în tabelul 6.5 considerând că
termenul planificat al realizării proiectului este de 32 săptămâni.
Tabel 6.5 Rezultatele aplicării algoritmului PERT pentru proiectul dat
|
Activitatea |
Denumireaactivită_ii. |
Durata |
Tij |
tij |
Termenul
min. de terminare al activ.(tj) |
Termenul
maxim de terminare al act. |
Dispersiaσij2 |
P(tj£Tij) |
||
|
|
|
aij |
mij |
bij |
|
|
|
|
|
|
|
(1,3) (1,2) (4,7) (4,6) (2,5) (2,12) (7,8) (6,9) (5,6) (5,10) (10,11) (10,12) (8,9) (8,13) (11,13) (1,4) (3,5) (12,13) |
A B C D E F G H I J K L M N Q Fictivă Fictivă Fictivă |
2 4 2 2 4 4 1 2 4 1 1 1 2 1 2 |
5 6 4 3 7 6 3 5 5 2 2 3 3 2 5 |
8 14 6 4 16 14 5 8 12 3 3 5 4 3 8 |
16 8 21 22 16 32 24 27 22 25 27 32 27 32 32 |
5 7 4 3 8 7 3 5 6 2 2 3 3 2 5 |
5 7 4 3 15 14 7 26 21 17 19 20 10 9 31 |
16 8 21 22 16 32 24 27 22 25 27 32 27 32 32 |
1 2,75 0,44 0,11 4 2,75 0,44 1,00 1,77 0,11 0,11 0,44 0,11 0,11 1,00 |
0,5 0,5 1,0 1,0 0,5 1,0 1,0 0,84 0,72 1,0 1,0 1,0 1,0 1,0 0,84 |
Așa cum se observă drumul critic
este dat de activitățile B, E, I, H, Q, durata totală de execuție a proiectului
este tn = 31 săptămâni,
dispersia duratei totale este σn2 = 2,75 + 4 + 1,77
+ 1,0 + 1 = 10,52 factorul de probabilitate este ![]() iar probabilitatea de
realizare a duratei planificate a proiectului este: p(tn
£ Tplan) = 0,617
iar probabilitatea de
realizare a duratei planificate a proiectului este: p(tn
£ Tplan) = 0,617
Ținând seama că graful are un număr
mic de activități, putem spune că avem o planificare justă a proiectului din
punct de vedere al termenului final planificat.
Analizând probabilitățile de
realizare la termene planificate ale activităților, observăm că pentru
activitățile A,B și E trebuie luate măsuri de urgentare a exercițiilor în
vederea realizării acestora la termenele planificate.
Observații.
Calculele PERT conduc la erori
destul de importante:
- ipoteza că durata medie a
proiectului este egală cu cea a drumului critic este incorectă. Durata totală
medie estimată prin calcule PERT este întotdeauna optimistă, adică este mai
mică decât cea reală. Cu cât există mai multe drumuri paralele într-o rețea și
cu cât diferențele dintre lungimile lor sunt mai mici, cu atât eroarea este mai
mare;
- metoda PERT oferă rezultate
corecte dacă: a) drumul critic al unui proiect este suficient de lung în
comparație cu oricare alt drum complet, astfel încât probabilitatea de a exista
un alt drum critic să fie practic neglijabilă; b) drumul critic are suficient
de multe activități astfel încât teorema limită centrală să poată fi aplicată.
Informațiile obținute în urma
calculelor PERT, nu sunt suficiente pentru conducătorul de proiect, deoarece
atenția acestuia va fi orientată spre activitățile de pe drumul critic, a căror
distribuție a fost înlocuită cu mediile lor, fără a acorda atenție și
celorlalte activități care în cazul nerealizării uneia la timpul mediu
calculat, pot produce perturbații mari în rețea (îndeosebi în cazul rețelelor
arborescente) mergând până acolo încât, determină un alt drum critic.
Modelul
de simulare PERT În definirea modelului pornim de la următoarele
considerente:
- activitățile (i,j) ale unui
proiect P, reprezentat prin rețeaua G, au duratele tij , care sunt
variabile aleatoare cu distribuții date;
- presupunem că duratele tij
sunt independent distribuite, fiecare cu un (ordin) interval de variație finit;
- se numește realizare a proiectului
P rețeaua G în care fiecare activitate (i,j) are o durată fixă, extrasă la
întâmplare din distribuția lui tij.
- fiecărei realizări îi corespunde
un drum critic și o durată totală stabilite în mod determinist.
Datele de bază cerute pentru
rezolvarea modelului propus sunt distribuțiile duratelor activităților. În
cazul unui proiect întâlnim cazuri practice în care, fie toate activitățile au
aceeași distribuție a duratelor (cazurile cele mai simple), fie că fiecărei
activități a rețelei îi corespunde un tip propriu de distribuție a duratei
(cazurile cele mai frecvente). Aceste date sunt obținute de la tehnicienii care
au ceva experiență în tipul de activități implicate sau prin metode ale
analizei dispersionale în care se ține seama de evoluțiile reale anterioare ale
duratelor fiecărei activități obținându-se astfel diferiți parametrii ai
distribuțiilor corespunzătoare activităților date (această a doua posibilitate
presupune însă un volum de calcule suplimentare, ceea ce ridică costul
rezolvării proiectului mărind însă exactitatea datelor obținute).
În ambele cazuri se consideră
suficiente pe lângă limitele domeniului de variație finit, media și dispersia
distribuțiilor utilizate pentru fiecare activitate în parte. Acești parametrii
(media și dispersia distribuției unei activități) pot fi obținuți impunând
niște condiții de realizare a duratelor fiecărei activități (de exemplu, o
probabilitate dată a estimărilor pe care le facem).
Metoda simulării Monte Carlo constă
în aplicarea algoritmului de calcul al drumului critic pentru un număr
suficient de mare de mulțimi de durate ale activităților (numărul acestora
fiind determinate de exactitatea rezultatelor pe care vrem să le obținem),
generate conform distribuțiilor corespunzătoare. Această tehnică poate fi
utilizată în două moduri de bază diferite.
Prima implică o mărime relativ mai
simplă și este pentru a testa, de exemplu, dacă media duratei a proiectului
µ, este sau nu realizată. Aceste teste statistice pot fi secvențiale și
implică aplicarea tehnicilor statistice standard. Această abordare are însă
dezavantajul că ea dă niște informații întâmplătoare despre distribuția duratei
proiectului.
A doua aplicație a tehnicii, oferă
foarte multă oportunitate și va fi considerată în cele ce urmează. Aceasta
presupune următorul algoritm de calcul:
Pasul 1. Se generează duratele aleatoare ale activităților
conform cu anumite distribuții date (Beta, lognormală, uniformă, normală,
triunghiulară) în intervalul [A,B], în orice fel de combinație. Această
flexibilitate permite, în particular, să încercăm diferite distribuții și să
observăm efectele ce se obțin în cazul neglijării sau luării în considerare a
distribuției fiecărei activități.
Pasul 2. Se calculează drumul critic, folosind metoda clasică,
găsindu-se activitățile critice și termenele activităților.
Pasul 3. Se determină duratele Ti de realizare a
proiectului. Se repetă etapele 1, 2, 3, de N ori, N suficient de mare. Media
µ și dispersia σT2 a duratei totale T a
lucrării, sunt date de formulele:
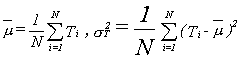
Pasul 4. Pentru fiecare activitate se determină indicele de
criticalitate: Cij = vij / N unde vij este
numărul care exprimă de câte ori activitatea (i,j) a fost activitate critică
din cele N cazuri studiate. Indicele de criticalitate al unei activități,
reprezintă probabilitatea ca acea activitate să fie critică.
Activitățile cu indicii Cij
mai mari, formează drumurile critice din graf.
Întrucât se consideră un număr
suficient de mare de realizări, teorema limită centrală, spune că este o foarte bună
aproximație normală cu media µx și dispersia σx2/N,
notată cu NOR(µx, σx2/N), unde
media pentru X, (variabila aleatoare corespunzătoare duratei proiectului) este
μx = M[x], iar σx2, reprezintă
dispersia lui X.
Este clar că valoarea lui N are
influență asupra gradului de exactitate al estimației lui μx.
Metode
de generare a variabilelor aleatoare de distribuții date specifice rețelelor
PERT. Modelul de mai sus,
presupune că duratele de execuție ale activităților sunt variabile aleatoare.
Dacă X este o astfel de variabilă ea trebuie să aibă următoarele proprietăți.
C1. SĂ fie mărginită, adică să
existe un interval finit astfel încât P(xÏ[A,B]) = 0.
C2. SĂ existe o valoare M cea mai
probabilă M
Î [A,B], adică X să fie o variabilă aleatoare unimodală.
C3. Din inegalitatea lui Cebâșev
rezultă că dacă μ = M[x], iar σ2 este dispersia lui X,
atunci ![]() ; de aceea se poate impune ca variabila de tip PERT să aibă
și proprietatea B - A = 6σ.
; de aceea se poate impune ca variabila de tip PERT să aibă
și proprietatea B - A = 6σ.
În problemele de tip
PERT în care duratele sunt aleatoare, intervin de obicei următoarele
distribuții ale duratelor activităților:
a) Distribuția uniformă, sau rectangulară, care are densitatea
|
|
b) Distribuția normală a cărei funcție de densitate este următoarea:
![]()
unde m și σ
desemnează parametrii distribuției. În cazul problemelor PERT, ne interesează
însă determinarea cu o probabilitate dată a parametrilor m și σ în
intervalul (a,b). În această situație vom avea:
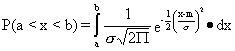
Punând ![]() 5, vom obține integrala lui Laplace:
5, vom obține integrala lui Laplace:
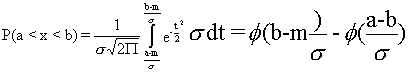
unde valorile lui
φ se obțin din tabele. Se demonstrează că punând
m = a+3σ,
atunci P(m-3σ < x <m + 3σ) = 0,99 adică, variabila aleatoare X
care urmează o lege normală aparține intervalului (a,b) cu o probabilitate
foarte aproape de unitate (regula celor trei sigma).
c) Distribuția lognormală. Variabila aleatoare Y se numește lognormală
dacă x = lny are o repartiție normală, adică:
![]()
De obicei, duratele activităților au
repartiții lognormale. Această variabilă nu satisface în mod riguros condiția
C1, însă se poate arăta că oricare ar fi ![]() 8, există un interval (A,B) astfel că
8, există un interval (A,B) astfel că ![]() 9.
9.
d) Distribuția Beta. O variabilă aleatoare V are repartiția Beta dacă
densitatea sa de repartiție este:
![]()
unde
|
|
Dar V nu satisface
condițiile C1 și C2 de mai sus; de aceea trebuie să facem transformarea W = (B-A)·V + A. Densitatea de
repartiție a variabilei W este:
|
|
|
|
(6.19)
Dăm în continuare, algoritmi de
generare a variabilelor de distribuție uniformă, normală, lognormală și beta
specifice problemelor Pert.
1. Generarea (variabilelor) duratelor aleatoare cu
distribuție uniformă, pe un interval
dat [A,B] presupune următorul algoritm:
a1 - se generează un
număr aleator uniform distribuit u
Î (0,1);
a2 - se consideră ca
durată a unei activități valoarea care se obține pentru X calculând expresia X
= A +(B-A)·u.
2. Pentru generarea unei variabile normale pe un interval dat [A,B], ținem seama de regula celor 3
sigma și de teorema limită centrală. Algoritmul în această situație presupune
următoarele etape:
a1 - Se calculează ![]()
a2 - Se calculează
µ = A + 3σ;
a3 - Se generează n=12
numere aleatoare u1,...,u12 uniforme pe (0,1) și
independente;
a4 - Se calculează ![]() . Variabila Z are o repartiție normală N(0,1), deoarece
pentru n=12, teorema limită centrală se poate considera adevărată;
. Variabila Z are o repartiție normală N(0,1), deoarece
pentru n=12, teorema limită centrală se poate considera adevărată;
a5 - Se calculează X =
µ + σ z. Se consideră valoarea lui X ca durată a activității în
cursul unei "realizări".
3. Pentru generarea unei variabile aleatoare lognormale pe un interval [A,B] dat se
aplică următorul algoritm:
a1 - Se calculează media m și dispersia s cu ajutorul formulelor următoare: ![]() unde σ și µ
sunt dispersia, respectiv media unei variabile normale pe [A,B];
unde σ și µ
sunt dispersia, respectiv media unei variabile normale pe [A,B];
a2 - Se calculează
µ1 și σ1 conform formulelor următoare:
![]() și
și ![]()
a3 - Se generează o
variabilă Z normală N(0,1) folosind procedeul arătat la punctul 2;
a4 - Se calculează y =
µ1+zσ1 (variabila y este normală N(µ1,
σ1));
a5 - Se calculează
(x=lny), variabila X este variabila lognormală generată.
4. Pentru generarea variabilelor de tip beta pe un interval [A,B] se șine seama
de următoarea teoremă: dacă x1
și x2 sunt variabile aleatoare independente de tip gama avâd
respectiv parametrii (p,λ), (q,λ) atunci variabila V = x1
/ (x1 + x2), este o variabilă beta de parametrii p și q.
Conform teoremei, generarea unei variabile beta se reduce la generarea a două
variabile de tip gama pentru λ dat.
Algoritmul este următorul:
a1 - se consideră că
(B-A)/6 și că μ = A + 3σT ipoteză presupusă adevărată în
cazul distribuției Beta;
a2 - se determină p și q
din relațiile (6.18) și (6.19);
a3 - se generează o
variabilă gama conform formulei x1 = - log(T1. T2
... Tp)/λ unde T1 T2 ...Tp
sunt p numere aleatoare uniforme pe (0,1);
a4 - Se generează a doua
variabilă gama utilizând formula
x2 =
-log(T1 ...Tq)/λ unde T1... Tq
au aceiași semnificație ca și T1 ...Tp.
a6 - variabila ![]() este variabila beta utilizată ca durată a unei
activități în calculul unei "realizări" a proiectului.
este variabila beta utilizată ca durată a unei
activități în calculul unei "realizări" a proiectului.
Analiza
performanțelor aplicării simulării Monte Carlo pentru determinarea duratelor a
unui proiect Rezolvarea grafului
din figura 6.11 și utilizând metoda PERT clasică, a dus la obținerea
următoarelor rezultate: durata proiectului este de 66.0 iar dispersia este
60.27, drumul critic trecând prin 1-2-4-5-9. Metoda Monte Carlo utilizând
10.000 realizări implică o medie de 67.0 ± 0.13 și o dispersie de 44.3
± 2 în cazul utilizării distribuției beta. În figura 6.11 sunt trecuți
indicii de criticalitate obținuți în urma aplicării metodei Monte Carlo.
Valorile acestora pot fi considerate ca o măsură utilă a gradului de atenție pe
care conducătorul proiectului, o acordă fiecărei activități a proiectului.
Notăm de asemenea faptul că activitățile 6-8 și 8-9 nu sunt niciodată critice.
De fapt, ele nu pot fi critice, dar algoritmul determinist nu ne poate da o
asemenea informație.
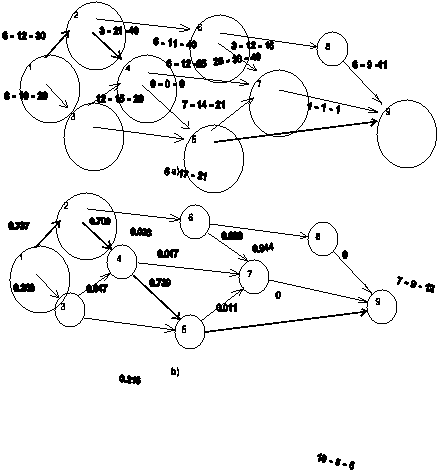
Fig.
6.4.
Notăm că abordarea statistică a
determinat același drum critic, însă prin simulare drumul critic a fost
determinat în condițiile în care s-a impus un grad de siguranță mult mai mare
decât în cazul modelului determinist, obținându-se totodată și un surplus de
informații.
Trebuie însă să arătăm că acest
exemplu constituie un caz simplu de graf întâlnit în practică. În realitate,
există rețele mult mai complexe pentru care simularea Monte Carlo oferă
rezultate mult mai interesante, rezolvând și înlăturând erorile pe care le
presupune metoda PERT calsică.
Practica simulării Monte Carlo în
determinarea duratelor de execuție a proiectelor a demonstrat că, foarte mult
timp, se consumă cu generarea numerelor aleatoare, astfel încât timpul de
rulare este esențial o funcție liniară de numerele aleatoare generate sau,
pentru o aceeași rețea, o funcție liniară de numărul activităților din rețea.
Aceste relații sunt adevărate pentru rețele foarte mari cu un grad mare de
arborescență. Pentru o rețea de 200 activități și 10.000 de cicluri de simulare
utilizând un program pentru IBM 7090, timpul de rulare a fost, în jur de 20 de
minute pentru distribuții triunghiulare și în jur de cinci minute pentru
distribuții uniforme. În cazul folosirii metodelor analitice timpul de rulare
crește exponențial cu numărul arcelor.
În scopul micșorării duratei de
rulare se propun diverse metode. Două dintre acestea ni se par mai interesante:
- se consideră realizarea obținută
prin punerea tuturor duratelor activităților la cel mai scăzut punct al șirului
de valori și găsim drumul critic corespunzător proiectului și durata lui, l.
Punem apoi toate duratele activităților care nu sunt pe drumul critic la
valoarea lor cea mai înaltă. Se determină activitățile care sunt pe drumurile
cu lungime mai mare decât l. Activitățile care n-au fost luate în considerare
după cele două teste sunt înlăturate, urmând numai pentru cele rămase să se
aplice simularea Monte Carlo;
- în cazul în care nu ne interesează distribuția exactă a duratei proiectului ci numai media și durata ei, activitățile care sunt întotddeauna critice sunt înlocuite cu activități deterministe cu duratele egale cu mediile distribuțiilor originale.