Matroizi şi funcţiilor submodulare
Propoziţie
:
Dacă M=(N, F) este un matroid atunci funcţia sa de cardinalitate este dată prin 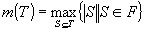 .
Dacă (N, F) este un sistem de independenţă pentru care funcţia de cardinalitate m(T) este submodulară atunci M=(N, F) este un matroid.
.
Dacă (N, F) este un sistem de independenţă pentru care funcţia de cardinalitate m(T) este submodulară atunci M=(N, F) este un matroid.
Dānd o mulţime finită N şi o funcţie submodulară şi nedescrescătoare f pe N, cu
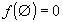 , politopul
, politopul 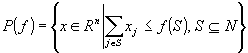 se numeşte polimatroidul asociat cu (N,f).
se numeşte polimatroidul asociat cu (N,f).
De asemenea, definim funcţia de rang polimatroid asociată cu P(f) printr-o funcţie
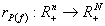 dată prin
dată prin 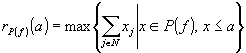 . Pentru rP(f) asociată cu polimatroidul P(f),
. Pentru rP(f) asociată cu polimatroidul P(f), 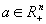 şi orice punct x maximal īn
şi orice punct x maximal īn 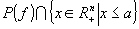 este satisfăcută relaţia
este satisfăcută relaţia 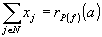 .
.
Propoziţie:
Dacă
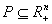 satisface condiţiile:
satisface condiţiile:
- dacă
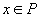 ,
, 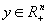 şi
şi 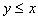 atunci
atunci 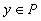 ;
pentru orice
;
pentru orice 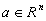 , dacă x1 şi x2 sunt puncte maximale în
, dacă x1 şi x2 sunt puncte maximale în 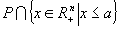 , atunci
, atunci 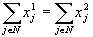 ,
,
atunci P este un polimatroid.
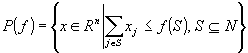 se numeşte polimatroidul asociat cu (N,f).
se numeşte polimatroidul asociat cu (N,f).
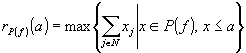 . Pentru rP(f) asociată cu polimatroidul P(f),
. Pentru rP(f) asociată cu polimatroidul P(f),