CIBERNETICĂ

1)

Un vânzător de fructe trebuie să decidă câte cutii cu fructe să cumpere ştiind că, dacă nu le va vinde în următoarele cinci zile, preţul lor va scădea cu 50%, la noul preţ găsind cu siguranţă cumpărători. Preţul de cumpărare al unei cutii este de 20 u.m. iar cel de vânzare de 25 u.m. cantitatea cerută (exprimată în cutii) este o variabilă aleatoare cu următoarea distribuţie de probabilitate:

Care este soluţia adoptată de decident în condiţiile în care el este indiferent faţă de risc?

a	)	3 cutii
b	)	5 cutii
c	)	6 cutii
d	)	7 cutii
e	)	4 cutii

- // -

2)

Se consideră problema:

Baza B = (a₂, a₄) cu B^-1 = (variabilele de abatere s-au notat x₃, x₄) este sigur optimală dacă:

a	)	c1 ³ 0
b	)	c1 Î (1, 2]
c	)	celelalte 4 afirmaţii sunt false
d	)	c1 ³ 2
e	)	c1 ³ 1,5

- // -

3)

Se considerã cã piaţa unui anumit produs este una normalã. Care dintre rezultatele urmãtoare, obţinute pe baza datelor statistice privind funcţiile inverse ale cererii şi respectiv ofertei , poate fi ales, oricare ar fi Q ³ 0?

a	)	p^D(Q) = -0,4Q + 2 p^S(Q) = -0,5Q – 5
b	)	p^D(Q) = -0,4Q + 7 p^S(Q) = 0,6Q + 4
c	)	p^D(Q) = 0,4Q + 3 p^S(Q) = 0,6Q – 4
d	)	p^D(Q) = -0,4Q + 6 p^S(Q) = 0,5Q – 3
e	)	p^D(Q) = -0,4Q + 3 p^S(Q) = 0,6Q - 4

- // -

4)

Într-o economie funcţia cererii de bani este: şi, la momentul iniţial, venitul real Y este 10000 iar rata dobânzii este 25%. De asemenea, oferta de bani M^S este iniţial egalã cu 4000. Dacã în perioada urmãtoare oferta de bani creşte cu 50% iar reglarea la echilibru se face prin nivelul preţurilor P, atunci rata inflaţiei va fi:

a	)	30%;
b	)	70%;
c	)	110%.
d	)	50%;
e	)	80%;

- // -

5)

Pe baza datelor statistice (Y_t, r_t, M_t) s-a identificat funcţia cererii de bani:

,

unde A este o constantă care se poate determina ştiind că nivelul de echilibru este Y^*=1.000, r^*=36% şi balanţa monetară reală . Atunci sensitivitatea cererii speculative de bani este:

a	)	150,5.
b	)	–347,2;
c	)	321,2;
d	)	– 257,8;
e	)	–250;

- // -

6)

Intr-o economie mică cu rată de schimb flexibilă descrisă de modelul: C = 125 + ; I = 200 – 10r ; NX = 150 – 5 e; T = 100 ; G = 150 ; Y = 1200 (venitul potenţial), se ştie că rata reală a dobânzii mondiale este 10%. Pentru a menţine echilibrul la nivelul outputului potential şi a aduce r la nivelul ratei mondiale, rata de schimb e trebuie să fie:

a	)	42,5 ;
b	)	30,5 ;
c	)	45 ;
d	)	20,5.
e	)	15 ;

- // -

7)

Se considerã o economie închisã, în care se cunosc urmãtoarele date: funcţia cererii de consum este , unde , -reprezintã venitul disponibil, Y-venitul oferit, T = 750 reprezintã impozitele şi taxele, I = 600 investiţiile la nivelul economiei şi G = 800 cheltuielile guvernamentale. Atunci, creşterea cheltuielilor guvernamentale cu 50 u.m.( ΔG=50 ) va induce o creştere a valorii de echilibru a lui Y cu:

a	)	9%.
b	)	7,5%;
c	)	4,5%;
d	)	6,3%;
e	)	3,5%;

- // -

8)

Fie un program liniar (P) în forma standard. Care afirmaţie NU este, în general, adevărată ?

a	)	Dacă în soluţia optimă a unui program liniar (P) apare o variabilă artificială cu valoare nenulă, atunci programul (P) nu are soluţii admisibile;
b	)	O soluţie dual-admisibilă este optimă dacă şi numai dacă este simultan primal şi dual admisibilă.
c	)	Dacă x^* este soluţie optimă de bază a problemei (P) asociată unei baze B şi u^* este soluţie optimă a problemei duale (D) atunci cBx^* = u^*b;
d	)	În orice soluţie optimă de bază a unui program liniar (P) numărul componentelor nenule este cel mult egal cu numărul restricţiilor problemei;
e	)	Fie () programul rezultat din (P) înlocuind vectorul termenilor liberi b cu . Fie B o bază optimă pentru programul (P) şi soluţia programului () asociată bazei B. Dacă verifică testul de optimalitate, din algoritmul simplex-primal, atunci este soluţie optimă a programului ();

- // -

9)

Pentru o firmă mijlocie s-a identificat funcţia de producţie Q_t = F(K_t,L_t), cu proprietatea că , unde E_K şi E_L sunt elasticităţile în raport cu factorii K_t şi L_t. Costurile reale ale factorilor sunt şi (- costul de oportunitate al capitalului şi - salariul nominal). Folosind modelul de fundamentare a deciziei optime pe termen lung având ca obiectiv maximizarea profitului brut al firmei şi aplicând condiţiile necesare de optim arătaţi că se poate determina:

a	)	numai Lt^*;
b	)	Lt^*, Kt^*, Qt^*;
c	)	nici una.
d	)	numai Kt^*;
e	)	Lt^*şi Kt^*;

- // -

10)

Pe o piaţă de capital cererea şi respectiv oferta pentru un activ financiar sunt estimate prin funcţii liniare în variabila preţ, adică – în timp continuu:

cu a, b > 0 şi cu g, d > 0.

Se consideră că variaţia preţului se poate scrie sub forma:

cu 0 <e <1.

Dacă preţul de echilibru este P^e iar preţul iniţial al activului este P₀ identificaţi, din traiectoria preţului ca soluţie a modelului de mai sus, componenta de care depinde stabilitatea (t Î [0, t_f])

a	)	P^e,
b	)	,
c	)	,
d	)	,
e	)	.

- // -

11)

Se considerã modelul lui Samuelson:

dat

cu a = 0,8 iar k = 2,5. Evoluţia indicatorului este:

a	)	uniformã şi stabilã;
b	)	uniformã şi instabilã;
c	)	descrisă de o variantă diferită de celelalte 4 variante.
d	)	alternantã în semn;
e	)	oscilantã şi instabilã;

- // -

12)

Utilizând modelul dinamic al lui Ludwig, pentru o firmă s-a determinat că:

unde  reprezintă venitul din vânzări, K – stocul de capital, a – rata amortizării (deprecierii) bunurilor capital şi r – rata dobânzii. În acest caz, este optim pentru firmă ca stocul de capital K să fie:

a	)	KY^*;
b	)	KY^* < K < KX^*;
c	)	KX^*;
d	)	KYX^*;
e	)	KYX^* < K < KX^*.

- // -

13)

O companie are un fond de investiţii de 500.000 u.m.Aceşti bani pot fi investiţi în obligaţiuni municipale cu o rată anuală a dobânzii de 5% sau într-un nou utilaj ce costă 500.000 u.m. Dacă se achiziţionează utilajul atunci, pentru o conjunctură economică favorabilă, se estimează un profit anual de 100.000 u.m., iar în cazul unei conjuncturi economice nefavorabile, se estimează o pierdere anuală de 20.000u.m. Pentru ce probabilitate asociată stării favorabile a economiei, agentul economic este indiferent între cele două variante?

a	)	p=0,375;
b	)	p=0,377;
c	)	p=0,372;
d	)	p=0.37.
e	)	p=0,357;

- // -

14)

Fie modelul:

Putem determina nivelul de echilibru al venitului Y(t) fără să cunoaştem valoarea lui l şi, dacă da, aceasta este:

a	)
b	)	Y^*= (1 – b)(a + I + G)
c	)
d	)	Nu putem
e	)

- // -

15)

Fie (P) un program liniar în care funcţia obiectiv se maximizează şi (P’) programul dedus din (P) prin adăugarea unei restricţii suplimentare. Presupunem că (P) şi (P’) au soluţii optime şi fie max P, max P’ valorile optime ale funcţiilor obiectiv din (P) respectiv (P’). Care din următoarele afirmaţii este ÎNTODEAUNA adevărată ?

a	)	max P = max P’;
b	)	max P ³ max P’;
c	)	max P > max P’;
d	)	max P £ max P’;
e	)	max P < max P’;

- // -

16)

Fie modelul macroeconomic descris, în timp discret, de relaţiile:

– cererea de consum C în funcţie de venitul disponibil Y ^d;

– taxele T în funcţie de venitul Y;

– cererea totală de bani în funcţie de rata dobânzii r şi venitul Y;

– investiţia I în funcţie de rata dobânzii r.

Pentru ansamblul parametrilor selectaţi varianta care ar putea fi aleasă respectând dependenţele economice cunoscute:

a	)	(0,65; 0,4; 0,6; – 0,3; – 0,2).
b	)	(0,7; – 0,3; 0,2; 0,4 ;1);
c	)	(– 0,7; 0,2; 0,1; – 0,5; 2);
d	)	(0,65; 1,3; 0,2; – 0,3; – 0,2);
e	)	(– 0,7; –0,2; 0,1; – 0,5; 0,8);

- // -

17)

Fie o piaţă cu două produse x₁ şi x₂. Nivelurile minime ale consumului celor două produse sunt =5u şi =4u, iar preţurile de vânzare p₁=5 u.b. şi p₂=3 u.b. Un cumpărător cu un venit mediu zilnic de 70 u.b. foloseşte o funcţie Bernoulli pentru a măsura utilitatea consumului celor două produse cu a₁=a₂=0,5. Se cere să se determine cantităţile optime din cele două produse ce trebuie cumpărate pentru a maximiza utilitatea consumului.

a	)	x1^* = 8,2; x 2^* = 9,5);
b	)	nici unul din celelalte 4 răspunsuri nu e corect.
c	)	x1^* = 9,5; x2^* = 8,3);
d	)	x1^* = 9,5; x2^* = 8,2);
e	)	x1^* = 8,3; x2^* = 9,5);

18)

Cinci decidenţi au exprimat următoarele preferinţe pentru cinci variante decizionale:

D₁: V₂>V₄>V₁>V₃>V₅

D₂: V₁>V₄>V₃>V₂>V₅

D₃: V₄>V₃>V₅>V₁>V₂

D₄: V₄>V₁>V₂>V₅>V₃

D₅: V₁>V₂>V₄>V₅>V₃

Să se de termine decizia colectivă prin metoda lui Condorcet.

a	)	V4 >^c V1 >^c V2 >^c V3 >^c V5.
b	)	V4 >^cV3 >^cV2>^cV1 >^cV5;
c	)	V2>^cV3 >^cV1>^cV4 >^cV5;
d	)	V3 >^cV4 >^cV5 >^cV2>^c V1;
e	)	V4 >^c V1 >^c V3 >^c V2 >^c V5;

- // -

19)

S-a constatat statistic că ecuaţia de dinamică (discretă) a venitului naţional Y este de forma:

unde G este variabila exogenǎ, cheltuieli guvernamentale.

Dacă se cunosc valorile iniţiale Y_–1 = 800 şi Y₀ = 850 iar G₁ = 400, care va fi, folosind relaţia de dinamică, venitul la momentul t = 2? (Se presupune că, cheltuielile guvernamentale se păstrează la acelaşi nivel)

a	)	2700;
b	)	2400;
c	)	1000.
d	)	850;
e	)	1200;

- // -

20)

Ratele de rentabilitate corespunzătoare acţiunilor A şi B au următoarea distribuţie:

Probabilitate Rata de rentabilitate (%)

RA RB

0,25 0 4

0,5 14 8

0,25 36 10

Ştiind că preţul unei acţiuni A este de 800 u.m. şi că preţul unei acţiuni B este de 400 u.m., care va fi rata de rentabilitate a portofoliului format din 10 acţiuni de tip A şi 5 de tip B?

a	)	14,9%;
b	)	nici un răspuns din celelalte 4 nu e corect.
c	)	11,9%;
d	)	12,9%;
e	)	13,9%;

- // -

21)

Se consideră problema maximizării venitului unei firme cu trei activităţi care utilizează două resurse:

Fie x₄ şi x₅ variabile ecart. În tabelul simplex final avem:

max		c	3	1	2	0	0
cB	B		a1	a2	a3	a4	a5
2	a3	30	3	0	1	1	1
1	a2	40	5	1	0	1	2

Dacă o nouă evaluare a disponibilului celor două resurse este dată de vectorul , care este efectul modificării ?

a	)	Soluţia este optimă cu fmax = 195.
b	)	Soluţia este optimă cu fmax = 225;
c	)	Problema modificată nu are soluţii admisibile;
d	)	nu verifică testul de optimalitate;
e	)	Baza B = (a3, a2) nu este optimă;

- // -

22)

S-a constatat, în urma unui studiu de marketing, că cererea şi oferta unui produs pot fi validate statistic ca funcţii liniare de preţul unitar al produsului mai precis:

– cererea D _t = a – b P_t cu a, b > 0 şi

– oferta S _t = – g + d P_{t– 1} cu g, d > 0 iar

Pentru reglarea preţului produsului se foloseşte funcţia excedent de cerere iar parametrul de reglare este 0 < e < 1.

Identificaţi răspunsul corect privind valoarea preţului de echilibru P ^e în condiţiile enunţate:

a	)	,
b	)	.
c	)	,
d	)	,
e	)	,

- // -

23)

La Bursa de Mărfuri Bucureşti s-au identificat, pe baza datelor statistice, funcţiile cererii şi ofertei unui produs (în mii tone/lună):

.

Mecanismul de ajustare a ofertei la cerere este de tip walrasian, cu viteza de ajustare , în timp continuu. Formulaţi modelul dinamicii preţului aşteptat al acestui produs (cu p₀=1) şi arătaţi că traiectoria de evoluţie este:

a	)	;
b	)	;
c	)	Nici una dintre variantele a), b), d), e).
d	)	;
e	)	;

- // -

24)

Se consideră un program liniar (P). După aducerea la forma standard şi adăugarea variabilelor artificiale s-a obţinut problema (FBP) căreia i s-a aplicat metoda Simplex. Să presupunem că în soluţia optimă a problemei (FBP) există cel puţin o variabilă artificială cu valoare nenulă. În această situaţie, care din următoarele răspunsuri este exact?

a	)	Programul (P) are soluţie optimă;
b	)	Programul (P) nu are soluţii admisibile;
c	)	Programul (P) are soluţii admisibile;
d	)	Mulţimea de soluţii admisibile a programului (P) este nemărginită.
e	)	Programul (P) are optim infinit;

- // -

25)

Fie problema de programare liniară

.

Considerăm x₄ şi x₅ variabilele ecart şi x₆ o variabilă artificială pentru a obţine forma extinsă. Pentru baza B = (a₃, a₁) se cunoaşte inversa .

Care este soluţia optimă a problemei duale ?

a	)	u1 =  1, u2 = -2;
b	)	u1 =  2, u2 =  1;
c	)	u1 = -2, u2 =  1;
d	)	u1 =  2, u2 = -1;
e	)	u1 = -1, u2 =  2;

- // -

26)

Care este prima aproximaţie a minimului global al funcţiei:

f(x) = + x₁x₂ + +x₁ + x₂

pe direcţia celei mai rapide descreşteri, luând ca punct iniţial x⁰ = (0, 0)^T?

a	)	x^1 = (–,–)^T;
b	)	x^1 = (–,)^T;
c	)	x^1 = (,)^T;
d	)	x^1 = x^0;
e	)	x^1 = (,–)^T;

27)

Se consideră următoarea problemă de maximizare a venitului unei firme cu trei activităţi care utilizează trei resurse:

În tabelul simplex optim avem:

Dacă disponibilul actual al resursei R₃ (care trebuie consumată în întregime) creşte cu o unitate atunci venitul maxim al firmei:

a	)	scade cu ;
b	)	creşte cu ;
c	)	nu se modifică.
d	)	creşte cu ;
e	)	creşte cu ;

- // -

28)

Se considerã următorul model al unei economii deschise mici:

unde G = 800. Presupunem cã rata de schimb este fixatã la e = 1 şi cã rata mondialã a dobânzii este , în timp ce Atunci, soldul balanţei comerciale la echilibru va fi:

a	)	NX = 421;
b	)	NX = –256;
c	)	NX = 0.
d	)	NX = –312;
e	)	NX = 329;

- // -

29)

Se consideră elementele:

cu ajutorul cărora se va construi un model liniar care să permită stabilirea unui program de fabricaţie corespunzător valorii maxime a venitului total, astfel încât resursele să nu fie depăşite (forma canonică).

Din tabelul:

		cj	3	4	6	0	0	0
c^B	B		a1	a2	a3	a4	a5	a6
6	a3	24	0	1/7	1	2/7	-1/7	0
3	a1	34	1	17/7	0	-1/7	4/7	0
0	a6	28	0	-9	0	0	-2	1

rezultă că:

a	)	(min)g = 246, unde g reprezintă funcţia obiectiv a problemei duale.
b	)	soluţia optimă este degenerată;
c	)	(a1,a3,a6) nu este bază optimală;
d	)	În soluţia optimă a dualei problemei considerate avem = 57/7;
e	)	resursa R3 cu disponibilul 212 este consumată în întregime prin programul optimal;

- // -

30)

Se consideră următoarea problemă de maximizare a venitului unei firme cu trei activităţi care utilizează trei resurse:

În tabelul simplex optim avem:

Între ce limite poate varia disponibilul b₁ al primei resurse astfel încât în programul optim de producţie să se menţină structura actuală? (disponibilul celorlalte două resurse rămân fixate la valorile indicate în (P)).

a	)	84 £ b1 £ 112;
b	)	92 £ b1 £ 148;
c	)	b1 ³ 130;
d	)	95 £ b1 £ 105;
e	)	b1 £ 92;

- // -

Observaţie: Fiecare subiect se punctează cu 3 puncte

Soluţii (vor fi completate în curând şi celelalte)

Întrebare	Răspuns
1	e
2
3
4
5	b
6
7
8
9	c
10
11
12
13	a
14
15
16
17	e
18	a
19
20	b
21
22
23	c
24
25
26
27
28
29
30
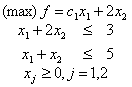
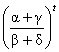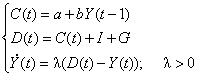
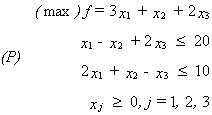
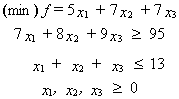