Vom spune că un domeniu poliedral nevid 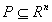este întreg dacă fiecare din feţele sale nevide conţine un punct întreg. În loc de utilizarea tuturor feţelor putem considera doar feţele minimale. Deoarece fiecare faţă minimală este un punct de extrem pentru domeniul poliedral dacă şi numai dacă rang(A)=n, vom putea spune că un domeniu poliedral 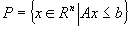cu rang(A)=n este întreg dacă şi numai dacă toate punctele sale de extrem sunt întregi.

Un sistem de inegaliţăti liniare 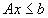este numit total întreg dual dacă pentru orice c întreg astfel încât problema de programare liniară 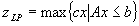peste domeniul poliedral P este finită şi duala sa 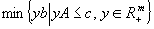are o soluţie optimă întreagă. Folosind această noţiune, avem că dacă 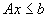este total întreg dual şi b este întreg atunci şi domeniul poliedral 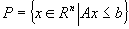este întreg.

Propoziţie:

Pentru un domeniu poliedral întreg complet dimensionat există o unică reprezentare printr-un sistem total întreg dual cu membru drept întreg.

urmator