O matrice A de dimensiune 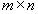este total unimodulară dacă determinantul fiecărei submatrici pătrate formate din A este –1, 0 sau 1. Pentru o astfel de matrice avem că 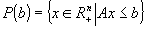este un domeniu poliedral întreg pentru orice 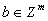pentru care 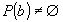. Acest lucru se poate generaliza pentru optimizarea combinatorială la enunţul:

Propoziţie:

Dacă A este o matrice total unimodulară, b, b’, d, d’ sunt întregi şi 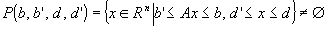atunci P(b, b’, d, d’) este un domeniu poliedral întreg.

Exemple de matrici evident unimodulare sunt:

• matricile de elemente 0, 1 şi –1 în care în fiecare coloană sau există o singură valoare nenulă, sau există două valori nenule din care una este 1 şi una –1.
• matricile interval
• matricile reţea

Matricile interval sunt matricile A de dimensiune 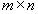şi elemente 0-1 în care, în fiecare coloană valorile 1 sunt consecutive, deci în care dacă a_ij=a_kj şi k>i+1 atunci a_sj=1 pentru orice s pentru care i<s<k.

Propoziţie:

1. Transpunere;
2. formatea matricii (A, I), unde I este matrice unitate;
3. ştergerea unei linii sau coloane unitare;
4. multiplicarea cu –1 a unei linii sau coloane;
5. interschimbarea a două linii sau coloane;
6. duplicarea liniilor sau coloanelor;
7. realizarea unei operaţii pivot;
8. compunerea a două matrici de formă specială.

urmator