Matrice reţea

O matrice reţea este o matrice în care coloanele reprezintă arcele unei matrici de incidenţă nod-arc pentru un digraf, după stergerea unei linii şi execuţia unui număr oarecare de pivotări simplex. Definirea exactă a matricilor reţea o vom da în continuare împreună cu elementele necesare prezentării ei.

Fie D=(V, F) un digraf cu m+1 noduri şi n arce şi A’ matricea de incidenţă nod-arc a digrafului presupus conex. Vom considera în plus că rang(A’)=m deoarece este convenabil să lucrăm cu matrici cu rangul egal cu numărul de linii.

Transformarea lui A’ se realizează prin:

  1. Fie A matricea de dimensiune care se obţine din A’ prin ştergerea oricărei linii.

  2. Fie A=(A1, A2) rescrierea lui A în care A1 este o matrice nesingulară a lui A de dimensiune . Arcele (e1, e2, …, em) corespunzătoare coloanelor lui A1 induc un arbore de trecere în D notat prin T=(V, F1).

  3. Reprezentarea unei coloane din A2, corespunzătoare unui arc ej=(u, v), este o combinaţie liniară a coloanelor din A1 şi este dată prin vectorul de incidenţă
pentru unicul drum pj din T de la u la v, definită prin:

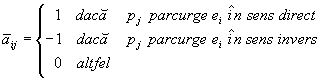
Dând un arbore orientat T=(V, F2) şi un digraf D=(V, F2) cu |V|=m+1, |F1|=m şi |F2|=n, matricea de incidenţă arc-drum notată cu M(T, D) corespunzătoare drumurilor din T care au punctele terminale definite prin arcele din F2 se numeşte matrice reţea.

urmator