Matrici total echilibrate
Fie Mk, 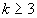 , familia de matrici de dimensiune
, familia de matrici de dimensiune 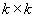
de elemente 0-1 pentru care suma pe linii şi pe coloane este egală cu 2 şi care nu conţin submatrici de forma 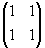 . Vom spune că o matrice cu elemente 0-1 este o matrice echilibrată dacă nu conţine nici o submatrice din M2k+1, pentru orice
. Vom spune că o matrice cu elemente 0-1 este o matrice echilibrată dacă nu conţine nici o submatrice din M2k+1, pentru orice 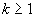 . Vom spune că o matrice de elemente 0-1 este total echilibrată dacă ea nu conţine nici o submatrice din Mk, orice
. Vom spune că o matrice de elemente 0-1 este total echilibrată dacă ea nu conţine nici o submatrice din Mk, orice 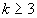 .
.
Problema generală de grupare se defineşte prin:
(FP) 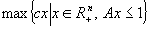
iar cea de acoperire drept:
(FC) 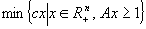
având astfel domeniile poliedrale 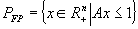
şi respectiv 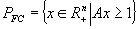 şi pentru ele putāndu-se asocia problemele duale:
şi pentru ele putāndu-se asocia problemele duale:
(DFP) 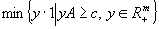
şi respectiv
(DFC) 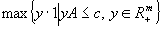 .
.
Teoremă
:
- Dacă A este o matrice total echilibrată atunci
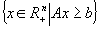 este īntreg şi (DFC) are o soluţie optimă īntreagă pentru orice
este īntreg şi (DFC) are o soluţie optimă īntreagă pentru orice 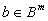 .
.
- Dacă A este o matrice total echilibrată atunci
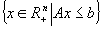 este īntreg şi (DFP) are o soluţie optimă īntreagă pentru orice
este īntreg şi (DFP) are o soluţie optimă īntreagă pentru orice 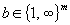
.
urmator
![]() , familia de matrici de dimensiune
, familia de matrici de dimensiune ![]()
![]()
![]()
![]()
![]()
![]() .
.