Fie N={1, 2, …,n} o mulţime finită şi F o mulţime de submulţimi ale lui N. P=(N, F) este un sistem de independenţă dacă pentru 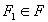şi 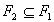avem şi 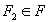. Elementele lui F se numesc mulţimi independente, celelalte submulţimi ale lui N numindu-se dependente.

Dând un sistem de independenţă P=(N, F), spunem că 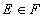este o mulţime de independenţă maximală dacă pentru orice 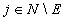avem 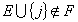. O mulţime de independenţă maximală T este un maxim dacă pentru orice 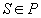avem 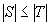. Pentru a desemna dimensiunea unei mulţimi de independenţă de cardinalitate maximă 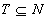, se foloseşte notaţia 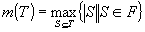. Trebuie remarcat că, dacă 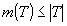şi 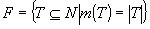, atunci P se poate specifica şi sub forma P=(N, m).

M=(N, F) este un matroid dacă M este un sistem de independenţă în care pentru orice submulţime 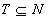, orice mulţime de independenţă din T care este maximă în T are cardinalitatea m(T).

urmator