Matroizi
Matroizi matriciali.
Fie A o matrice de dimensiune 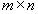
şi N mulţimea indicilor coloanelor din A. Definim sistemul de independenţă (N, F) prin 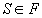 dacă mulţimea coloanelor date prin S conţine doar coloane liniar independente. Pentru fiecare submatrice AT având coloanele aj pentru
dacă mulţimea coloanelor date prin S conţine doar coloane liniar independente. Pentru fiecare submatrice AT având coloanele aj pentru 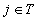 se ştie că fiecare mulţime maximă de coloane liniar independente conţine m(T)=rang(AT) coloane şi astfel (N, F) este un matroid.
se ştie că fiecare mulţime maximă de coloane liniar independente conţine m(T)=rang(AT) coloane şi astfel (N, F) este un matroid.
În general, dacă M este un matroid şi există o matrice A astfel încât mulţimile de independenţă ale lui M corespund coloanelor liniar independente ale lui A, atunci M este numit matroid matricial.
Matroizi grafici.
Fie G=(V, E) un graf şi
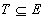 o submulţime de muchii.
o submulţime de muchii. 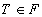 dacă subgraful GT=(V, T) nu conţine cicluri. Ştim că pentru orice
dacă subgraful GT=(V, T) nu conţine cicluri. Ştim că pentru orice 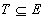 , cardinalitatea unei mulţimi maxime de muchii care este aciclică în GT este m(T)=|V|-c, unde c este numărul componentelor conexe ale lui GT, şi astfel, (E, F) este un matroid.
, cardinalitatea unei mulţimi maxime de muchii care este aciclică în GT este m(T)=|V|-c, unde c este numărul componentelor conexe ale lui GT, şi astfel, (E, F) este un matroid.
În general, dacă M este un matroid şi există un graf G astfel încât mulţimile de independenţă ale lui M corespund mulţimilor de arce aciclice din G, atunci M se numeşte matroid grafic.
Trebuie observat că matroizii grafici sunt în acelaşi timp şi matroizi matriciali.
Matroizi partiţie.
Fie Ej, 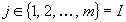
, m mulţimi finite şi disjuncte două câte două şi 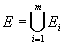 .
. 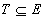 este o mulţime de independenţă dacă pentru orice
este o mulţime de independenţă dacă pentru orice 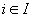
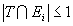 .
.
Pentru orice 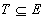
, cardinalitatea unei mulţimi de independenţă maximală din T este 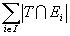 şi astfel (E,F) este un matroid.
şi astfel (E,F) este un matroid.
În general, dacă M este un matroid şi există o mulţime E cu partiţia {E
1,E2,…Em} astfel încât mulţimile de independenţă ale lui M corespund mulţimilor de independenţă din E, atunci spunem că M este un matroid partiţie.
urmator
![]()
![]()
![]()